Структурный
| Тип используемого конечного элемента
|
Оболочка (Shell)
|
| Тип граничных условий
|
Жесткое защемление боковой грани и равномерно распределенная нагрузка
|
| Возможности
|
Получение: резонансной частоты, формы колебаний на резонансной частоте и ускорения на заданном интервале частот.
|
Рис. 6
Порядок выполнения работы:
1. Определяем тип анализа:
MAIN MENU => PREFERENCES…=> STRUCTURAL=> ОК.
1. Выполняем следующую последовательность действий:
M.M. => PREFERENCES… => STRUCTURAL
=> OK. Таким образом, фильтруется все меню под структурный расчет.
2. Задаем свойства материалов и определяемся с типом элементов.
Выбираем тип элементов:
M.M. =>
PREPROCESSSOR =>
ELEMENT TYPE =>
ADD/EDIT/DELETE
=>
ADD…=>
STRUCTURAL SHELL ELASTUC 4 NODE 63 =>
OK
=>
CLOSE. Сначала определяем толщины используемых пластин, для этого:
M.M. =>
PREPROCESSOR
=>
REAL CONSTANTS =>
ADD/EDIT/DELETE =>
ADD =>
ОК и в пункте
SHELL THICKNESS AT NODE I TK(I) задаем толщину пластины равную
0,006 метрам и повторяем операцию
ADD =>
ОК, задаем толщину второго материала равную
0,012 метрам . Далее задаём свойства материалов:
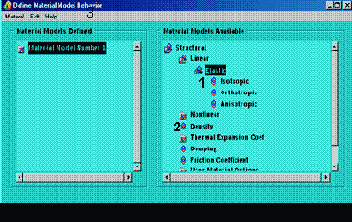
M.M. => PREPROCESSSOR => MATERIAL PROPS => MATERIAL MODELS. Затем, следуя цифрам на рис. 7, выполняем следующие действия:
А. Двойным нажатием мыши на указанные папки выполняем:
STRUCTURAL => LINEAR => ELASTIC => ISOTROPIC. В окне LINEAR ISOTROPIC PROPERTIES FOR MATERIAL NUMBER 1 задаем: модуль Юнга EX = 2е11 Па
и коэффициент Пуассона PRXY = 0,27.
Б. Аналогично раскройте DENSITY и в поле плотность DENS
задайте 7800 кг/м3.

В. Нажмите: А. M.M. => PREPROCESSOR => MODELING
–CREATE– => –AREAS– RECTANGLE => BY DIMENSIONS…, вводим координаты углов: X1 = -0.5, X2 = 0.5, Y1 = 0, Y2 = 1, нажимаем APPLY;



 M.M. => PREPROCESSOR => MODELING –CREATE– => –AREAS– RECTANGLE => BY DIMENSIONS… - X1 = -0.3, X2 = 0.3, Y1 = 0, Y2 = 0.5.
M.M. => PREPROCESSOR => MODELING –CREATE– => –AREAS– RECTANGLE => BY DIMENSIONS… - X1 = -0.3, X2 = 0.3, Y1 = 0, Y2 = 0.5. Г. Проводим расчет:
Г. Проводим расчет: Б. Строим графики:
Б. Строим графики: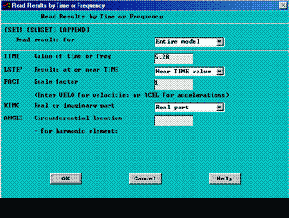 Г. Строим графики ускорений ранее выбранного одного узла. При гармоническом анализе ускорение представляет собой произведение перемещения на квадрат частоты. Т.е. для получения ускорений достаточно произвести простое перемножение:
Г. Строим графики ускорений ранее выбранного одного узла. При гармоническом анализе ускорение представляет собой произведение перемещения на квадрат частоты. Т.е. для получения ускорений достаточно произвести простое перемножение:
 M.M. => PREFERENCES => –MODELING– CREATE
=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.5 и 0, 0.75 соответственно. Нажимаем ОК.
M.M. => PREFERENCES => –MODELING– CREATE
=> –AREAS– RECTANGLE => BY DIMENSIONS… и задаем координаты X1, X2 и Y1, Y2 равные 0, 0.5 и 0, 0.75 соответственно. Нажимаем ОК. А. Задаем средний размер грани конечных элементов:
А. Задаем средний размер грани конечных элементов: M.M. => SOLUTION => –SOLVE– CURRENT LS
=> OK.
M.M. => SOLUTION => –SOLVE– CURRENT LS
=> OK.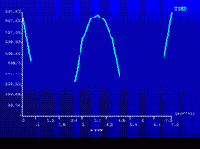
 Вводим в M.M.
=>GENERAL POSTPROC =>PLOT RESULTS =>PATH OPERATIONS
=>– PLOT PATH ITEM– ON GRAPH выбираем TFSUM и нажимаем, ОК. В результате получаем график представленный на рисунке 29.
Вводим в M.M.
=>GENERAL POSTPROC =>PLOT RESULTS =>PATH OPERATIONS
=>– PLOT PATH ITEM– ON GRAPH выбираем TFSUM и нажимаем, ОК. В результате получаем график представленный на рисунке 29.